8.8 Hypothesis Tests for a Population Proportion

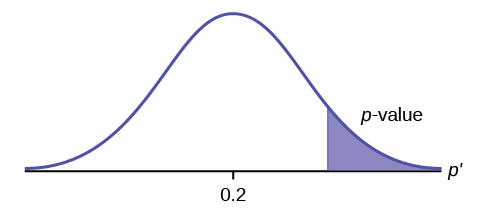
Because the alternative hypothesis is a [latex]\gt[/latex], this is a right-tail test. The p-value is the area in the right-tail of the distribution.

EXAMPLE

Suppose the hypotheses for a hypothesis test are:

[latex]\begin H_0: & & p=50 \% \\ H_a: & & p \neq 50\% \end[/latex]

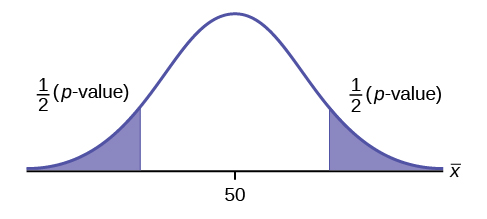
Because the alternative hypothesis is a [latex]\neq[/latex], this is a two-tail test. The p-value is the sum of the areas in the two tails of the distribution. Each tail contains exactly half of the p-value.

EXAMPLE

Suppose the hypotheses for a hypothesis test are:

[latex]\begin H_0: & & p=10\% \\ H_a: & & p \lt 10\% \end[/latex]

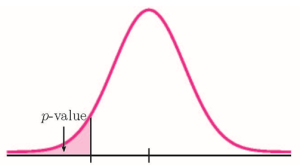
Because the alternative hypothesis is a [latex]\lt[/latex], this is a left-tail test. The p-value is the area in the left-tail of the distribution.

Steps to Conduct a Hypothesis Test for a Population Proportion

1. Write down the null and alternative hypotheses in terms of the population proportion [latex]p[/latex]. Include appropriate units with the values of the proportion.
2. Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
3. Collect the sample information for the test and identify the significance level.
4. Find the p-value (the area in the corresponding tail) for the test using the appropriate distribution:
   • If [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex], use the normal distribution with [latex]\displaystyle-p>>>>[/latex].
   • If one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex], use a binomial distribution.
5. Compare the p-value to the significance level and state the outcome of the test:
   • If p-value[latex]\leq \alpha[/latex], reject [latex]H_0[/latex] in favour of [latex]H_a[/latex].
     • The results of the sample data are significant. There is sufficient evidence to conclude that the null hypothesis [latex]H_0[/latex] is an incorrect belief and that the alternative hypothesis [latex]H_a[/latex] is most likely correct.
   • If p-value[latex]\gt \alpha[/latex], do not reject [latex]H_0[/latex].
     • The results of the sample data are not significant. There is not sufficient evidence to conclude that the alternative hypothesis [latex]H_a[/latex] may be correct.
6. Write down a concluding sentence specific to the context of the question.

USING EXCEL TO CALCULE THE P-VALUE FOR A HYPOTHESIS TEST ON A POPULATION PROPORTION

The p-value for a hypothesis test on a population proportion is the area in the tail(s) of distribution of the sample proportion. If both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex], use the normal distribution to find the p-value. If at least one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex], use the binomial distribution to find the p-value.

If both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex]:

• The p-value is the area in the tail(s) of a normal distribution, so the norm.dist(x,[latex]\mu[/latex],[latex]\sigma[/latex],logic operator) function can be used to calculate the p-value.
  • For x, enter the value for [latex]\hat

    [/latex].

  • For [latex]\mu[/latex], enter the mean of the sample proportions [latex]p[/latex]. Note: Because the test is run assuming the null hypothesis is true, the value for [latex]p[/latex] is the claim from the null hypothesis.
  • For [latex]\sigma[/latex], enter the standard error of the proportions [latex]\displaystyle>>[/latex].
  • For the logic operator, enter true. Note: Because we are calculating the area under the curve, we always enter true for the logic operator.

  If at least one of [latex]n \times p \lt 5[/latex] or [latex]n \times (1-p) \lt 5[/latex]:

  • The p-value is found using the binomial distribution.
  • If the alternative hypothesis is a [latex]\lt[/latex], the p-value is the probability of getting at most [latex]x[/latex] successes in [latex]n[/latex]trials where the probability of success is the claim about the population proportion [latex]p[/latex] in the null hypothesis.
    • The p-value is the output from the binom.dist(x,n,p,logic operator) function:
      • For x, enter the number of successes.
      • For n, enter the sample size.
      • For p, enter the the value of the population proportion [latex]p[/latex] from the null hypothesis.
      • For the logic operator, enter true. Note: Because we are calculating an at most probability, the logic operator is always true.
      • The p-value is the output from the 1-binom.dist(x-1,n,p,logic operator) function:
        • For x, enter the number of successes.
        • For n, enter the sample size.
        • For p, enter the the value of the population proportion [latex]p[/latex] in the null hypothesis.
        • For the logic operator, enter true. Note: Because we are calculating an at least probability, the logic operator is always true.

        EXAMPLE

        Marketers believe that 92% of adults own a cell phone. A cell phone manufacturer believes that number is actually lower. In a sample of 200 adults, 87% own a cell phone. At the 1% significance level, determine if the proportion of adults that own a cell phone is lower than the marketers’ claim.

        Solution:

        Hypotheses:

        From the question, we have [latex]n=200[/latex], [latex]\hat

        =0.87[/latex], and [latex]\alpha=0.01[/latex].

        To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.92[/latex]).

        [latex]\begin n \times p & = & 200 \times 0.92=184 \geq 5 \\ n \times (1-p) & = & 200 \times (1-0.92)=16 \geq 5\end[/latex]

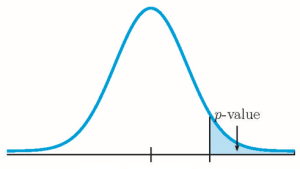
        Because both [latex]n \times p \geq 5[/latex] and [latex]n \times (1-p) \geq 5[/latex] we use a normal distribution to calculate the p-value. Because the alternative hypothesis is a [latex]\lt[/latex], the p-value is the area in the left tail of the distribution.

        

        

        Function	binom.dist	Answer
        Field 1	45	0.2710
        Field 2	50
        Field 3	0.93
        Field 4	true

        So the p-value[latex]=0.2710[/latex].

        Conclusion:

        Because p-value[latex]=0.2710 \gt 0.01=\alpha[/latex], we do not reject the null hypothesis. At the 1% significance level there is not enough evidence to suggest that the proportion of visitors who make a purchase is lower than 93%.

        NOTES

        1. The null hypothesis [latex]p=93\%[/latex] is the claim that 93% of visitors to the website make a purchase.
        2. The alternative hypothesis [latex]p \lt 93\%[/latex] is the claim that less than 93% of visitors to the website make a purchase.
        3. The p-value is the binomial probability of getting at most 45 successes (the number in the sample with the characteristic of interest) in 50 trials (the sample size) with a probability of success of 93% (the value of [latex]p[/latex] in the null hypothesis). In the calculation of the p-value:
           • The function is binom.dist because we are finding the probability of at most 45 successes.
           • Field 1 is the number of successes [latex]x[/latex].
           • Field 2 is the sample size [latex]n[/latex].
           • Field 3 is the probability of success [latex]p[/latex]. This is the claim about the population proportion made in the null hypothesis, so that means we assume [latex]p=0.93[/latex].
        4. The p-value of 0.2710 tells us that under the assumption that 93% of visitors make a purchase (the null hypothesis), there is a 27.10% chance that the number of visitors in a sample of 50 who make a purchase is 45 or less. This is a large probability compared to the significance level, and so is likely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely correct, and so the conclusion of the test is to not reject the null hypothesis. In other words, the proportion of visitors to the website who make a purchase adults is most likely 93%.

        EXAMPLE

        A drug company claims that only 4% of people who take their new drug experience any side effects from the drug. A researcher believes that the percent is higher than drug company’s claim. The researcher takes a sample of 80 people who take the drug and finds that 10% of the people in the sample experience side effects from the drug. At the 5% significance level, determine if the proportion of people who experience side effects from taking the drug is higher than claimed.

        Solution:

        Hypotheses:

        From the question, we have [latex]n=80[/latex], [latex]\hat

        =0.1[/latex], and [latex]\alpha=0.05[/latex].

        To determine the distribution, we check [latex]n \times p[/latex] and [latex]n \times (1-p)[/latex]. For the value of [latex]p[/latex], we use the claim from the null hypothesis ([latex]p=0.04[/latex]).

        [latex]\begin n \times p & = & 80 \times 0.04=3.2 \lt 5\end[/latex]

        Because [latex]n \times p \lt 5[/latex] we use a binomial distribution to calculate the p-value. Because the alternative hypothesis is a [latex]\gt[/latex], the p-value is the probability of getting at least 8 successes in 80 trials. (Note: In the sample of size 80, 10% have the characteristic of interest, so this means that [latex]80 \times 0.1=8[/latex] people in the sample have the characteristic of interest.)

        Function	1-binom.dist	Answer
        Field 1	7	0.0147
        Field 2	80
        Field 3	0.04
        Field 4	true

        So the p-value[latex]=0.0147[/latex].

        Conclusion:

        Because p-value[latex]=0.0147 \lt 0.05=\alpha[/latex], we reject the null hypothesis in favour of the alternative hypothesis. At the 5% significance level there is enough evidence to suggest that the proportion of people who experience side effects from taking the drug is higher than 4%.

        NOTES

        1. The null hypothesis [latex]p=4\%[/latex] is the claim that 4% of the people experience side effects from taking the drug.
        2. The alternative hypothesis [latex]p \gt 4\%[/latex] is the claim that more than 4% of the people experience side effects from taking the drug.
        3. The p-value is the binomial probability of getting at least 8 successes (the number in the sample with the characteristic of interest) in 80 trials (the sample size) with a probability of success of 4% (the value of [latex]p[/latex] in the null hypothesis). In the calculation of the p-value:
           • The function is 1-binom.dist because we are finding the probability of at least 8 successes.
           • Field 1 is [latex]x-1[/latex] where [latex]x[/latex] is the number of successes. In this case, we are using the compliment rule to change the probability of at least 8 successes into 1 minus the probability of at most 7 successes.
           • Field 2 is the sample size [latex]n[/latex].
           • Field 3 is the probability of success [latex]p[/latex]. This is the claim about the population proportion made in the null hypothesis, so that means we assume [latex]p=0.04[/latex].
        4. The p-value of 0.0147 tells us that under the assumption that 4% of people experience side effects (the null hypothesis), there is a 1.47% chance that the number of people in a sample of 80 who experience side effects is 8 or more. This is a small probability compared to the significance level, and so is unlikely to happen assuming the null hypothesis is true. This suggests that the assumption that the null hypothesis is true is most likely incorrect, and so the conclusion of the test is to reject the null hypothesis in favour of the alternative hypothesis. In other words, the proportion of people who experience side effects is most likely greater than 4%.

        Concept Review

        The hypothesis test for a population proportion is a well-established process:

        1. Write down the null and alternative hypotheses in terms of the population proportion [latex]p[/latex]. Include appropriate units with the values of the proportion.
        2. Use the form of the alternative hypothesis to determine if the test is left-tailed, right-tailed, or two-tailed.
        3. Collect the sample information for the test and identify the significance level.
        4. Find the p-value (the area in the corresponding tail) for the test using the appropriate distribution (normal or binomial).
        5. Compare the p-value to the significance level and state the outcome of the test.
        6. Write down a concluding sentence specific to the context of the question.